¿Cómo se calculan las valoraciones en Amazon?

Raúl Rivilla Bastante (@rrbastante). Licenciado en matemáticas y profesor del IES Fray Andrés de Puertollano.– Estoy seguro de que muchos de quienes lean estas líneas pueden haberse hecho esta pregunta alguna vez. Normalmente, Amazon (o muchas otras empresas tecnológicas que catalogan productos, viajes, actuaciones…  según la valoración recibida por sus usuarios) ofrece una información como ésta:

Probablemente, se haya auto-respondido pensando que la empresa hace una media de las puntuaciones, es decir, sumar las 3.576 opiniones de sus clientes y dividir por 3.576. Con la información que nos proporciona esa tabla, podríamos hacer eso de dos formas:

1ª Convirtiendo los porcentajes en cantidades: 50% de las 3576 opiniones con 5 estrellas, entonces hay 1788 votos con un 5, y así sucesivamente con 4, 3, 2 y 1 estrella.

2ª Trabajando con los porcentajes directamente. Es más rápido y el resultado es equivalente, obtendríamos:

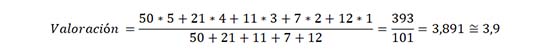
Técnicamente se llama una medía ponderada. Es una variante de la clásica media aritmética que todo el mundo aprende en primaria para calcular su nota media. La primera curiosidad es que las puntuaciones no sumen un 100% sino un 101%. Evidentemente esos porcentajes que nos ofrece Amazon en la tabla  no será exactos, tendrán decimales y fruto del redondeo a veces sumarán 100% pero otras será 101% o 99%. Por otra parte, la diferencia entre el valor obtenido y el publicado por Amazon es muy pequeña teniendo en cuenta que no hemos podido trabajar con los datos exactos (no tenemos las 3.576 opiniones, ni los porcentajes precisos) sino con aproximaciones. De hecho, la valoración que hemos obtenido es (redondeando) la misma que Amazon. No obstante, en la imagen que le ofrecía al principio, verá que hay una pestaña:

Precisamente hoy, tuve tiempo (y curiosidad suficiente)  como para pinchar en esa opción. Esperaba leer una explicación sobre esa media ponderada y tenía curiosidad por ver cómo sería. Sin embargo, lo que me encontré fue:

La verdad es que la explicación impresiona “modelo de programación de máquina”… tiene en cuenta factores como la antigüedad de la reseña, la utilidad de los votos de los clientes y si las reseñas son de compras verificadas

La pregunta es… ¿Algoritmo o vacile?

Bueno, lo primero que hice fue coger unos cuantos productos que estaban en las Ofertas flash del día para no ser yo quien los eligiera.

Por otra parte, intenté coger productos que tuvieran una variedad en la cantidad de opiniones que recogían. Desde unas decenas a varios miles. A continuación, calculé la valoración media ponderada con la información que proporcionaba Amazon. Estos fueron los resultados

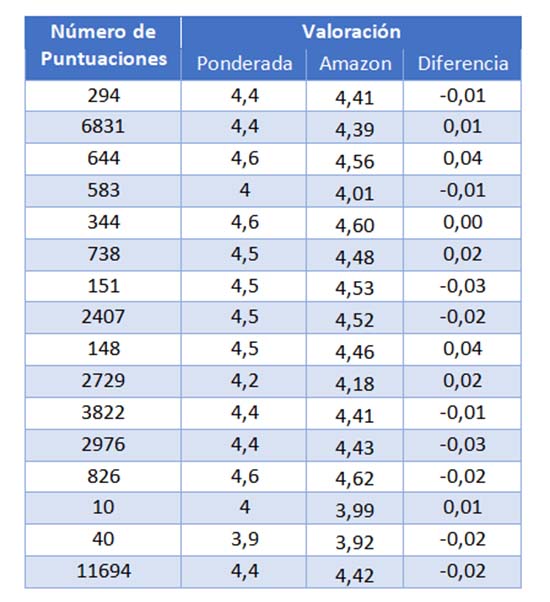
Para ilustrar los datos de esta tabla, he construido el siguiente gráfico:

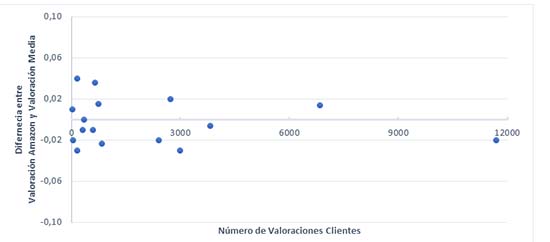
En este gráfico podemos apreciar como la diferencia entre ambas puntuaciones es de tan solo unas centésimas que con la regla del redondeo desaparecerían. Por otra parte, dado que no tenemos la información completa sobre las puntuaciones sino tan solo una pequeña tabla resumen es lógico que existan estas pequeñas imprecisiones que verdaderamente son mínimas.

Observe que aún con esta pequeña muestra lo que si parece apreciarse es que cuantas más valoraciones tiene un producto menor es la diferencia entre ambas puntuaciones, más cerca de 0 está. Esto se debe a una propiedad matemática de la media, la consistencia. La media eEs un estimador tanto más robusto cuantos más datos se utilizan para calcularla

Además, el coeficiente de correlación de Pearson[1] entre ambas puntuaciones es de 0,995. Tenga en cuenta que el máximo sería 1, solo alcanzable si las dos variables fueran exactamente iguales.

El algoritmo, el “modelo de programación de máquina”, del que habla Amazon, no parece tener efectos importantes. Por otra parte, la información que proporciona Amazon sobre su algoritmo  habla de que las opiniones más recientes son tenidas más en cuenta que las más antiguas.

Del producto que cogimos como ejemplo al principio, con 3.576 valoraciones y valor asignado por Amazon como 3,9 (con el valor medio obteníamos ), si le pedimos a la web que nos muestre las últimas opiniones de clientes, en este caso nos muestra 13 opiniones

Como vemos, la media de estas últimas 13 opiniones está cerca (0,0177) de la valoración global que asigna Amazon (3,9) y de la media global que hemos obtenido (3,891), eso es porque estas 13 últimas opiniones constituyen una buena muestra del conjunto, son aleatorias.

Pero si siguiendo la pauta de Amazon, quisiéramos prestar más importancia a las opiniones más recientes, ese tipo de cálculos podrían corresponderse con series temporales. Hay modelos muy variados y ricos que se utilizan en multitud de contextos diferentes. Es un campo relativamente moderno y en expansión. No obstante, para ilustrar algo tan sencillo voy a utilizar un modelo de serie temporal muy básico:

 A la valoración más reciente se le da un peso alfa (α), a la siguiente un peso α², a la siguiente un peso α³, y así sucesivamente. Si α es un número entre 0 y 1, cada término de la sucesión que se forma α, α², α³,… es menor que el anterior y por tanto, pueden usarse para calcular una media ponderada en el que la valoración más reciente es la más importante, y conforme las opiniones se alejan en el tiempo van perdiendo importancia. Ahora bien, ¿cómo de rápido van perdiendo importancia? Pues depende del valor de α. Veámoslo un ejemplo:

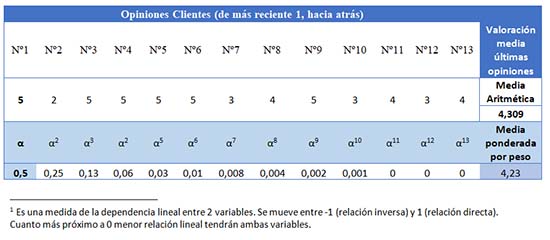
Con este valor de α = 0,5 = ½. La mitad de la opinión (50%)  se debería a la opinión más reciente, la última. La penúltima opinión valdría la mitad que la anterior (25%) y así sucesivamente. Esta sucesión de pesos es decreciente y con bastante rapidez. De las 3576 opiniones que teníamos, casi toda la opinión la deciden las 4 más recientes y la influencia a partir de la décima es prácticamente nula.

No tenemos más información que esas últimas 13 valoraciones que nos ha proporcionado Amazon, no obstante, si quisiéramos que la importancia de las opiniones no decreciera tan rápido hay dos caminos:

-Cuanto más próximo a 1 fuera el valor de alfa, más lentamente decrecería la sucesión. Por ejemplo,

-Cuanto más lentamente crecieran los exponentes, más lentamente disminuiría la sucesión. Por ejemplo,

Evidentemente pueden combinarse ambos criterios y elegir una sucesión de bases y otras de exponentes. Ahora bien, no parece plausible que se haga esa multitud de cálculos para una opinión que en realidad no está tan alejada de la simple y vieja media aritmética. Sería como matar moscas a cañonazos.

Así pues, como consumidor me inclino a pensar que quizá no haya un cálculo tan sofisticado y secreto como se nos cuenta. En el mejor de los casos se calculará la valoración teniendo en cuenta solo usuarios que hagan con regularidad compras y se tengan constancia de su pago y entrega para evitar bots que “inflen” o “hundan” valoraciones de forma interesada. Pero por lo demás, probablemente sea una simple y sencilla media de opiniones como usted y yo pensábamos que era.

No obstante, le recomiendo que como consumidor valore cada artículo que compre en ésta o cualquier otra web para colaborar con el resto de consumidores en dar (o quitar) confianza a aquellos que la merezcan (o no).

La respuesta, por tanto, a la pregunta que hacíamos es que probablemente sea un pequeño algoritmo muy vacilón para venderse como algo muy sofisticado.

Como contrapunto, la información que ofrece Amazon sobre la valoración de una de sus empresas colaboradoras, es mucho menos “sofisticada”. Por ejemplo, en ese producto que a modo de ejemplo seguíamos desde el principio:

Si pinchamos para tener mayor información, encontramos:

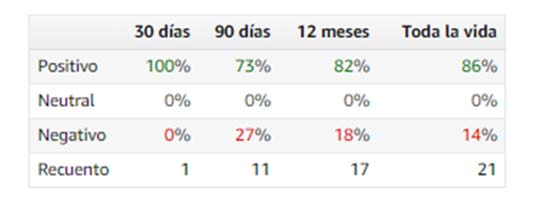
Tan solo nos ofrece una tabla en la que nos muestra cuantas opiniones ha tenido positivas, neutrales o negativas dicha empresa en determinado período de tiempo. Ahora bien, ¿qué considera Amazon opinión Positiva? ¿5 estrellas? Intuyo, al igual que usted, que probablemente 4 o 5 estrellas, 3 sería la calificación neutra y 1 o 2 las calificaciones negativas, pero … ¿no debería estar claro?

Por otra parte, esta tabla ofrece una información precisa y ya es cuestión que valoremos como clientes que nivel de confianza nos ofrece esa empresa. Al igual que antes, me permito recordarle, esas valoraciones serán tanto más fiables cuantas más opiniones reflejen. Es mucho más fácil manipular una opinión hecha con 10 votos que con 100 y esta a su vez más sencilla de manipular que si fueran 1000. En cualquier caso, piense en ello al hacer un pedido en esta o cualquier otra web.

[1] Es una medida de la dependencia lineal entre 2 variables. Se mueve entre -1 (relación inversa) y 1 (relación directa). Cuanto más próximo a 0 menor relación lineal tendrán ambas variables.