El método proporcional es la forma más justa de repartir escaños. Sin embargo, pesa sobre él una terrible maldición, como la del faraón, que lo condena ante los ojos de matemáticos, politólogos y expertos varios. Esa maldición se llama paradoja de Alabama. Aviso para navegantes: este texto no va de política, sino, sobre todo, de matemáticas electorales.
Me ha parecido interesante escribir sobre esto porque ilustra uno de los problemas que tenemos los seres humanos, y no sólo en nuestro país: la falta de pensamiento propio, de espíritu crítico, la aceptación sistemática de los dogmas -sin cuestionarlos- si nos vienen de figuras con autoridad.
La paradoja de Alabama se considera unánimemente como un defecto del método proporcional, hasta el punto que, para muchos, lo hace menos válido que otros tan injustos como el método D’Hondt.
Y así se enseña, supongo, en las universidades. Nuestros catedráticos, nuestros licenciados, nuestros expertos, nuestras mentes más formadas. Todos dando por cierto, y transmitiendo de generación en generación, una valoración errónea acerca de un procedimiento matemático que, para más inri, es muy, muy básico.
Al grano: ¿qué es la paradoja de Alabama?
Lo explico a continuación, pero si lo preferís, os voy a pasar un vídeo donde una matemática, Guadalupe Castellano, explica el método D’Hondt y el método proporcional –«por la regla de tres»-, paradoja de Alabama incluida. Es una explicación muy buena, y sencilla, y muy correcta en cuanto a lo matemático. Pero incorrecta en cuanto a trasladar lo teórico a la vida real.
Lo cuento aquí igualmente, con un ejemplo -el mismo que usa la matemática del vídeo-:
Tenemos 521.000 votos divididos entre 6 candidaturas. Y queremos repartir 8 escaños de la manera más proporcional posible.
Para ello los repartimos mediante reglas de tres, a razón de un escaño cada 65.125 votos. Los asignamos:
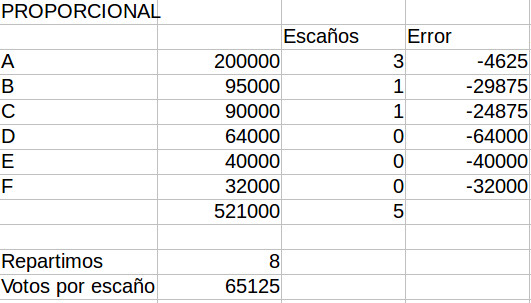
Y nos encontramos con que sólo hemos asignado 5 escaños. Y ya ningún partido tiene 65.125 votos disponibles. Nos faltan 3 escaños.
La columna “Error” contiene la cantidad de votos que están “huérfanos” de escaño. La forma más justa de repartir esos 3 escaños es asignárselos a las candidaturas que tienen más votos sin cubrir (esto es, a los “restos mayores”). Que son D, E, y F. La cosa quedaría así:
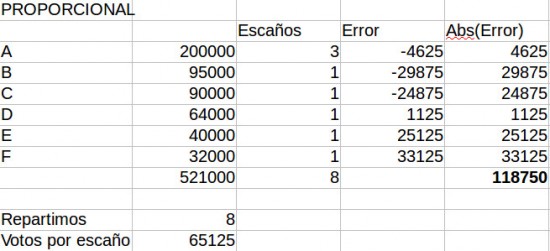
Y ya tenemos repartidos los 8 escaños.
Como podemos ver, el método proporcional tiene error, un error de redondeo (118.750 votos mal representados, el 23% del total). Esto sucede porque no se puede ajustar a la perfección 8 escaños entre 6 candidaturas y 521.000 votos.
Y además, es un error importante -8 escaños son demasiado pocos: a medida que aumentan los escaños, el error tiende, con altibajos, a disminuir-.
Pero, en cualquier caso, el método proporcional minimiza el error. Con D’Hondt sería de 193.750 votos (37%).
Sin embargo, está la paradoja de Alabama.
Para saber lo que es la paradoja de Alabama, vamos a utilizar este mismo ejemplo, con los mismos votos, pero vamos a repartir ahora 9 escaños. El resultado es este:
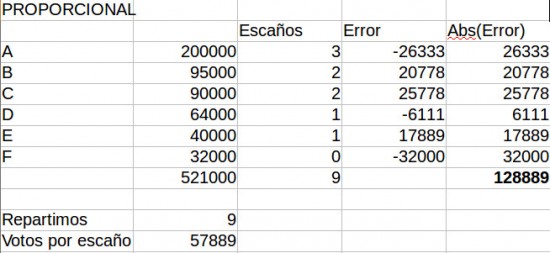
Y, sorpresa, sorpresa, mirad lo que le ha ocurrido a la candidatura F.
Antes, repartiendo 8 escaños, le tocaba 1.
Ahora, repartiendo 9 escaños, no le toca ninguno.
Repartiendo más, le tocan menos. Parece ilógico, ¿no? Ahí está la paradoja.
Y también parece injusto.
Aunque en realidad, no lo es. Es una ilusión. Pero una ilusión que ha «engañado» a sabios y expertos desde 1880, que es cuando se descubrió este “problema”.
Una ilusión que ha bastado para condenar al método proporcional.
¿Dónde está el problema?
Si os fijáis en la candidatura F, en el primer caso, con 8 escaños, resulta que le tocó uno con sólo 32.000 votos, pese a que el escaño valía 65.125 votos.
Esto es, la candidatura F está muy sobrerepresentada. El error de redondeo le ha beneficiado, y mucho. Se podría decir que ha tenido esa suerte. A alguna le tenía que tocar beneficiarse por el error de redondeo más que las demás.
Cuando repartimos 9 escaños, toca uno para cada 57.889 escaños. Y ese hecho cambia las asignaciones -a D le toca el sexto escaño directamente-, y también los restos que sobran del reparto inicial de escaños. El tercer mayor resto, que antes era la candidatura F, ahora es la C, que es la que recibe el error de redondeo a su favor.
A la F, en cambio, le ha tocado ser la más perjudicada. De nuevo, a alguna le tenía que tocar. Mala suerte.
Pero este hecho no supone ningún problema añadido. Es una consecuencia de que el error existe, y no se puede evitar. Ese error a veces beneficia a unos y perjudica a otros… y otras veces, es al contrario.
Pero eso no altera el hecho de que el método proporcional es el que menos error tiene. Es el más justo. Con paradoja de Alabama, o sin ella.
Si usamos el método D’Hondt para repartir 9 escaños, el error que sale es de 156.222 votantes mal representados. En el proporcional, con paradoja, el error es de 128.889.
El proporcional es mejor.
Y eso no es todo. La metedura de pata de los sabios y expertos es todavía mayor. Porque la paradoja de Alabama no sólo no es algo negativo, sino que, en realidad, cuando aparece, puede ser muy beneficiosa. Me explico:
Imaginémonos dos elecciones consecutivas. En una se reparten 8 escaños, en la siguiente, 9. Pero los votos son los mismos, los de este ejemplo.
En el primer periodo, la candidatura F ha estado muy sobrerepresentada. Sus votantes han tenido más peso que el que realmente les correspondía.
En el segundo periodo, la candidatura F ha estado infrarepresentada, más o menos, en el mismo grado.
Esto es, el error del primer periodo se ha compensado en el segundo. Lo que se le dio de más antes, se le quitó después. Tomados en conjunto los dos periodos, el error, en el caso de la candidatura F, prácticamente ha desaparecido.
En conclusión: la paradoja de Alabama, en este caso, ha sido beneficiosa. Ha reducido, y mucho, el déficit de representatividad:
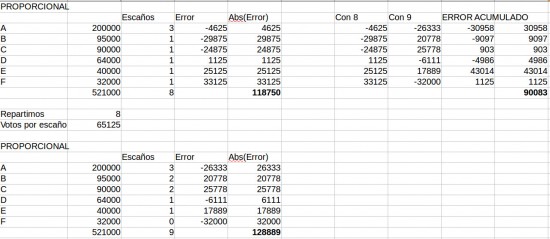
En el primer periodo, el déficit de representatividad era de 118.750 votantes. En el segundo, 128.889. Pero tomados los dos en conjunto, al producirse la paradoja de Alabama, el déficit acumulado baja hasta los 90.083 votos. 45.041 votos de error de media por periodo electoral.
Si hacemos lo mismo con el método D’Hondt, sale un déficit acumulado de 297.972 votos. Más del triple.
Y, por seguir comparando, con el método Sainte-Laguë, sale 204.056.
No hay color.
La maldición del método proporcional no existe. Es una ilusión. La paradoja de Alabama, de ser algo, sería, o podría ser, en algunos casos, una bendición.
Así que, si hay que repartir escaños -que no tendríamos por qué, pero bueno, si hay que hacerlo-, el método es el proporcional. El de la regla de tres.
Porque es el mejor. Porque es el más justo.
Y si viene con paradoja, pues que venga. Mejor aún.
Y en cuanto a los expertos y sabios… y a los matemáticos… parece mentira que 135 años después de descubrir la paradoja… todavía sigan creyendo -y transmitiendo-, que es un problema. Un dogma de fe que se refuta con matemáticas elementales.
Manda huevos.
P.D. Que no sé yo si es sólo un problema de no saber, o también de no querer. Voy a ser mal pensado, para variar:
En el vídeo (minuto 12:40), cuando la entrevistadora le pregunta a la matemática si el método D’Hondt es más justo que el proporcional, no es capaz de responder que sí. Tartamudea.
¿Duda? ¿Le traiciona la conciencia? ¿Es buena matemática, pero mala mentirosa?
Al final, no afirma que sí, pero lo defiende de todas maneras, con un “…al menos, no tiene la paradoja de Alabama”.
Esto es, “¡que viene el Coco!”
Gonzalo Plaza
Ciudadano en blanco
